Collaborative Filtering 基于物品或用户的协同过滤算法

内容较多，如果文章有错误，欢迎指出，以便于及时修正。

什么是协同过滤算法

协同过滤（Collaborative Filtering, CF）是一种常见的推荐算法，广泛用于个性化推荐系统，比如电商、视频平台、音乐推荐等。
它的核心思想是基于用户的历史行为或相似用户的行为，来预测用户可能感兴趣的内容，而不依赖于任何物品附加信息(如物品形状等)或用户附加信息(年龄，性别等)。
目前应用广泛的协同过滤算法主要所基于邻域的方法，有两种:

1. 基于用户的协同过滤算法(User-based CF) - 相似的用户喜欢相似的物品
2. 基于物品的协同过滤算法(Item-based CF) - 用户会喜欢与他们之前喜欢的物品所相似的物品

用到的核心

1. 相似度计算

   • 余弦相似度
   • 皮尔逊相关系数
   • 杰卡德相似度

2. 预测评分

   • 基于用户的协同过滤算法（本文）
   • 基于物品的协同过滤算法（本文）
   • 降维优化，梯度下降优化（ALS, SGD），采用矩阵分解（SVD[奇异值分解]、NMF[非负矩阵分解]） 降低计算复杂度，解决数据稀疏问题。（非本文介绍内容）

余弦相似度（Cosine Similarity）

余弦相似度是一种用于衡量两个向量相似程度的方法，它通过计算两个向量夹角的余弦值来表示它们的相似度，值域在[−1,1] 之间。
余弦相似度计算公式(由于博客对LaTex公式解析有点小问题，后续公式全部以截图形式展示)

取值范围:

• 1: 两个向量完全相拟，方向相同，夹角0度。
• 0: 两个向量完全无关，夹角90度。
• -1: 两个向量完全相反，夹角180度。

在推荐系统中，范围在[0,1]之间，负值通常不考虑。
Python代码示例:

import numpy as np
from sklearn.metrics.pairwise import cosine_similarity


def my_cosine_similarity(vec1, vec2):
    dot_product = np.dot(A, B)  # 计算点积
    norm_A = np.linalg.norm(A)  # 计算 A 的模
    norm_B = np.linalg.norm(B)  # 计算 B 的模
    cos_sim = dot_product / (norm_A * norm_B)  # 计算余弦相似度
    return cos_sim


# 定义两个向量
A = np.array([1, 2, 3])
B = np.array([2, 3, 4])

# 方法 1: numpy手撕
print("手动计算余弦相似度:", my_cosine_similarity(A, B))

# 方法 2: 使用 sklearn
cos_sim_sklearn = cosine_similarity([A], [B])[0, 0]
print("sklearn 计算余弦相似度:", cos_sim_sklearn)

输出:

手动计算余弦相似度: 0.9925833339709303
sklearn 计算余弦相似度: 0.9925833339709303

皮尔逊相关系数（Pearson Correlation）

皮尔逊相关系数（Pearson Correlation Coefficient，简称 PCC）是用于衡量两个变量之间线性相关性的指标，取值范围在[−1,1] 之间。

皮尔逊相关系数𝑟的值在[−1,1] 之间，含义如下：

• 𝑟 = 1: 完全正相关，X 增加时 Y 也一定增加（严格的正线性关系）。
• 𝑟 > 0: 正相关，X 增加时 Y 大概率 也增加。
• 𝑟 = 0: 无相关性，X 和 Y 之间 无线性关系。
• 𝑟 < 0: 负相关，X 增加时 Y 大概率 减少。
• 𝑟 = -1: 完全负相关，X 增加时 Y 一定 减少（严格的负线性关系）。

Python代码示例:

import numpy as np
from scipy.stats import pearsonr
from decimal import Decimal, getcontext

# 定义两个变量的数据
X = np.array([1, 2, 3, 4, 5])
Y = np.array([2, 3, 4, 5, 6])


def my_pearsonr_plus(X, Y):
    """
    高精度
    """
    getcontext().prec = 30  # 设置 Decimal 计算的结果精度（30位小数）,当然自己根据实际情况来设置精度，使用Decimal类型后默认无损失

    # 将数据转换为 Decimal 类型
    X = np.array([1, 2, 3, 4, 5], dtype=np.float64)
    Y = np.array([2, 3, 4, 5, 6], dtype=np.float64)
    X_decimal = [Decimal(x) for x in X]
    Y_decimal = [Decimal(y) for y in Y]

    # 计算均值
    X_mean = sum(X_decimal) / len(X_decimal)
    Y_mean = sum(Y_decimal) / len(Y_decimal)

    # 计算分子
    numerator = sum((x - X_mean) * (y - Y_mean) for x, y in zip(X_decimal, Y_decimal))

    # 计算分母
    denominator_X = sum((x - X_mean) ** 2 for x in X_decimal).sqrt()
    denominator_Y = sum((y - Y_mean) ** 2 for y in Y_decimal).sqrt()

    pearson_corr = numerator / (denominator_X * denominator_Y)

    return pearson_corr


def my_pearsonr(X, Y):
    """
    精度损失
    """
    X_mean = np.mean(X)
    Y_mean = np.mean(Y)

    # 计算分子
    numerator = np.sum((X - X_mean) * (Y - Y_mean))
    # 计算坟墓
    denominator = np.sqrt(np.sum((X - X_mean) ** 2)) * np.sqrt(np.sum((Y - Y_mean) ** 2))

    pearson_corr = numerator / denominator
    return pearson_corr


# 方法1：手撕。手撕不做精度优化可能会有精度问题，实际应用请优先使用封装好的库。手撕仅为学习展示。
print("手动计算皮尔逊相关系数(精度损失):", my_pearsonr(X, Y))
print("手动计算皮尔逊相关系数(高精度):", my_pearsonr_plus(X, Y))

# 方法 2：使用 SciPy 计算皮尔逊相关系数
corr, _ = pearsonr(X, Y)
print("SciPy 计算皮尔逊相关系数:", corr)

输出:

手动计算皮尔逊相关系数(精度损失): 0.9999999999999998
手动计算皮尔逊相关系数(高精度): 1.00000000000000000000000000000
SciPy 计算皮尔逊相关系数: 1.0

杰卡德相似度（Jaccard Similarity）

杰卡德相似度（Jaccard Similarity）是一种用于衡量 两个集合之间相似性 的指标，核心思想是衡量两个集合的交集在它们的并集中所占的比例。
通常适用于集合(Set)数据，比如标签集，关键词集，用户兴趣等等。

这个比较简单，不做过多解释。

Python代码示例：

def jaccard_similarity(set1, set2):
    intersection = len(set1.intersection(set2))
    union = len(set1.union(set2))
    return intersection / union


def jaccard_similarity_text(text1, text2):
    """
    用于文本相似度
    """
    set1 = set(text1.split())  # 按单词分割
    set2 = set(text2.split())
    return len(set1 & set2) / len(set1 | set2)


A = {1, 2, 3, 4, 5, 6}
B = {2, 3, 4, 5, 6, 7}
print("Jaccard 相似度:", jaccard_similarity(A, B))

text1 = "I love machine learning"
text2 = "I love deep learning"
print("Jaccard 文本相似度:", jaccard_similarity_text(text1, text2))

输出:

Jaccard 相似度: 0.7142857142857143
Jaccard 文本相似度: 0.6

杰卡德距离

P.S.: 扩展，杰卡德距离（Jaccard Distance）
有时候，我们需要计算两个集合的“差异性”，可以使用 杰卡德距离：
D(A,B) = 1 - J(A,B)
J(A,B)也就是上图所示的杰卡德指数。

基于用户的协同过滤（User-Based CF）

思路：找到和目标用户相似的其他用户，并推荐他们喜欢的物品。

实现步骤：

1. 计算用户之间的相似度（如余弦相似度、皮尔逊相关系数等）。
2. 找到与目标用户最相似的若干个用户（邻居）。
3. 通过邻居的喜好来预测目标用户可能喜欢的物品。

优缺点：
优点：适用于数据较稀疏的场景，能挖掘出一些长尾用户的兴趣。
缺点：当用户数量增多时，计算用户相似度的开销较大；且如果新用户没有历史数据，无法推荐（冷启动问题）。

首先准备属于源（数据清洗过后的数据）:
以景区推荐系统为例，我们需要准备用户对不同景区的评分，分数范围为0-5颗星。
其中行代表景区，列代表评分用户的昵称(用户名)，短横-代表该用户没有去过该地区，也就是我们的待推荐区。
(当然实际情况可能会有用户去过但是未打分的情况，这种情况不在本文讨论范围)
我们的目标是如何给用户名为小溪边的猫的用户，推荐2个最适合他的风景区。

	望云山风景区	幽谷仙境公园	七星湖度假村	龙吟峡谷探险区	雾隐古镇	碧波湖游览区
旅行侠客	5	5	2	1	5	3
云端漫步者	5	4	1	4	4	2
独行探险家	1	2	5	3	2	5
快乐旅人99	3	5	1	2	4	5
小溪边的猫	4	5	1	-	-	-

首先计算用户相似度，找出与小溪边的猫相似的N个用户(相似度计算已在本文前面提供了3种计算方式，这里不做赘述)，然后按照如下规则进行推荐:
根据这N个用户对景区的打分，如果与小溪边的猫用户相似的用户都选择了雾隐古镇，则我们把雾隐古镇推荐给小溪边的猫，同理，如果相似的用户都选择了碧波湖游览区，则我们给其推荐碧波湖游览区。
相似度计算已介绍过，接下来我们把重点放在最终结果预测上。
常用的方式之一是, 通过加权平均法（Weighted Sum）预测用户对物品的评分,预测公式如下:

如果要考虑的相对更全面一点，可以使用另一种方式，均值中心化加权平均（Mean-Centered Weighted Sum），预测公式如下:

主要目的是为了消除用户评分尺度不统一的影响，避免有人习惯打高分，有人习惯打低分。

当然除了以上两种方式，还有如下几种，简单列出几个，不过并不常用（不在本文详细讨论）。

• 直接平均法(适用于数据较少的情况，但准确性不高)
• 回归模型预测评分(适用于大规模数据，但是计算成本高)
• 矩阵分解(基于用户评分矩阵进行降维，学习用户和物品的隐含特征，并用其预测评分，适用于大规模推荐系统)

这里我们相似度选用皮尔逊相关系数，预测方式模型选用均值中心化加权平均来进行计算。
首先计算小溪边的猫的均值:

	望云山风景区	幽谷仙境公园	七星湖度假村	龙吟峡谷探险区	雾隐古镇	碧波湖游览区
小溪边的猫	4	5	1	-	-	-

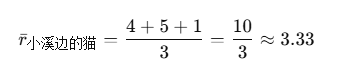
计算小溪边的猫与旅行侠客皮尔逊相关系数(还是公式问题，直接上图了):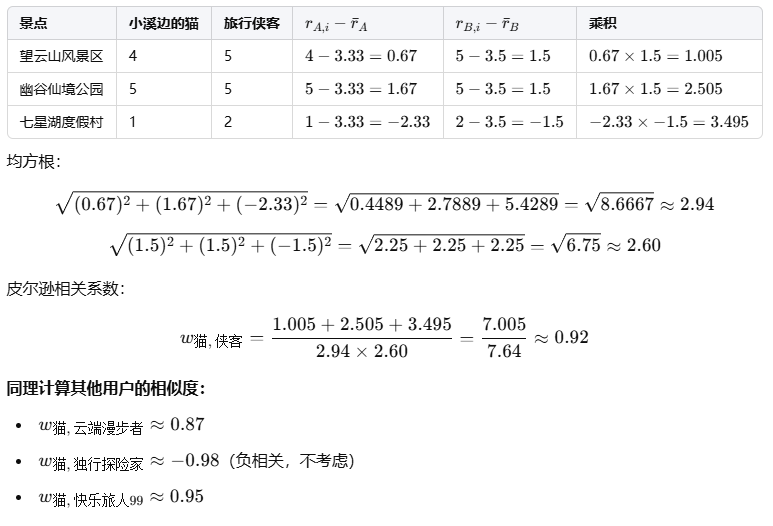

接下来使用均值中心化加权平均推理预测评分:
我们使用旅行侠客、云端漫步者、快乐旅人99，因为独行探险家负相关，影响预测准确性，所以不选用他。

用户	龙吟峡谷探险区评分	平均评分
旅行侠客	1	3.5
云端漫步者	4	3.33
快乐旅人99	2	3.0

所以最终预测评分为2.36，同理对另外两个景区进行评分，将得分最好的2个景区推荐给小溪边的猫，即可完成我们的任务。
注意，由于手算进行了四舍五入的精度损失，最终预测评分可能跟程序运行出来的稍有偏差

基于物品的协同过滤（Item-Based CF）

思路：如果两个物品被同一批用户喜欢，那么它们是相似的。对于目标用户，推荐与他之前喜欢的物品相似的物品。

实现步骤：

1. 计算物品之间的相似度（如余弦相似度、杰卡德相似度等）。
2. 找到与用户喜欢的物品相似的其他物品。
3. 结合用户的偏好，推荐用户可能喜欢的物品。

优缺点：
优点：相对稳定，适用于物品数量较多但用户数量较少的场景（比如电商推荐）。
缺点：需要计算物品相似度矩阵，可能会随着物品增长而变得庞大。

首先准备数据源（数据清洗过后的）:
依然所以景区推荐系统为例，我们需要准备用户对不同景区的评分，分数范围为0-5颗星。
其中行代表评分用户的昵称(用户名)，列代表景区，短横-代表该用户没有去过该地区，也就是我们的待推荐区。
我们的目标是如何将景区碧波湖游览区推荐给没有来过的用户，推荐2个最适合该风景区的用户。

	旅行侠客	云端漫步者	独行探险家	快乐旅人99	小溪边的猫
望云山风景区	5	5	1	3	4
幽谷仙境公园	5	4	2	5	5
七星湖度假村	2	1	5	1	1
龙吟峡谷探险区	1	4	3	2	2
雾隐古镇	5	4	2	4	5
碧波湖游览区	3	2	-	-	-

首先计算物品(景区)相似度，找出与龙吟峡谷探险区相似的N个景区(相似度计算已在本文前面提供了3种计算方式，这里不做赘述)，然后按照如下规则进行推荐:
比如说望云山风景区和碧波湖游览区有很大相似度，那么ItemCF会认为喜欢景区望云山风景区的用户也大可能喜欢碧波湖游览区，所以同样可以给予每个用户对该景区(物品)的打分来向量化物品。
相似度计算已介绍过，接下来我们把重点放在最终结果预测上。
结果预测的方式也已经介绍过了，不再赘述，开始手撕。

首先计算每个景点的均值:

	旅行侠客	云端漫步者	独行探险家	快乐旅人99	小溪边的猫	均值
望云山风景区	5	5	1	3	4	(5+5+1+3+4)/5=3.6
幽谷仙境公园	5	4	2	5	5	(5+4+2+5+5)/5=4.2
七星湖度假村	2	1	5	1	1	(2+1+5+1+1)/5=2.0
龙吟峡谷探险区	1	4	3	2	2	(1+4+3+2+2)/5=2.4
雾隐古镇	5	4	2	4	5	(5+4+2+4+5)/5=4.0
碧波湖游览区	3	2	-	-	-	-

然后计算碧波湖游览区与其他景点的相关性，以望云山风景区为例

已评分用户均值中心化:

用户	碧波湖游览区	望云山风景区	均值中心化
旅行侠客	3	5	3 - 3.6 = -0.6, 5 - 3.6 = 1.4
云端漫步者	2	5	2 - 3.6 = -1.6, 5 - 3.6 = 1.4

同理可得到碧波湖浏览区与其他景点的相关性，如下:

预测用户评分:

所以最终预测评分为4.30，同理对其他用户进行评分，将景区碧波湖游览区推荐给得分最好的2个用户，即可完成我们的任务。
注意，由于手算进行了四舍五入的精度损失，最终预测评分可能跟程序运行出来的稍有偏差

完整景区案例Python代码

基于物品的协同过滤推荐算法的景区推荐系统
不要偷懒，你只需要用python把公式带入就是实现啦。
暂不贴出来。当然你如果想要付费获取，我很乐意，请邮箱联系我。(邮箱在主页个人头像下面)

协同过滤局限性

冷启动问题: 新用户或新物品没有足够的历史数据，难以计算相似性。
数据稀疏问题: 用户与物品的交互数据通常是稀疏的，可能导致推荐质量下降。
可扩展性问题: 当用户或物品数量增加时，相似度计算和存储会变得昂贵。